lorentz-force
A simulator of the effect of a magnetic force in an electric field, built with numpy and pyplot.
Parameters are hard-coded into the file; the area where they should be modified is clearly delineated, and the importance of the various variables are noted in the comments. Especially relevant is the comment on the limitation of the correctness of Euler's method of numerical integration; users should be careful to set their step size small enough to combat the existence of artifactual spiraling in what should be uniform circular motion--e.g. what occurs in a constant magnetic field.
B Fields
Here are some example outputs:
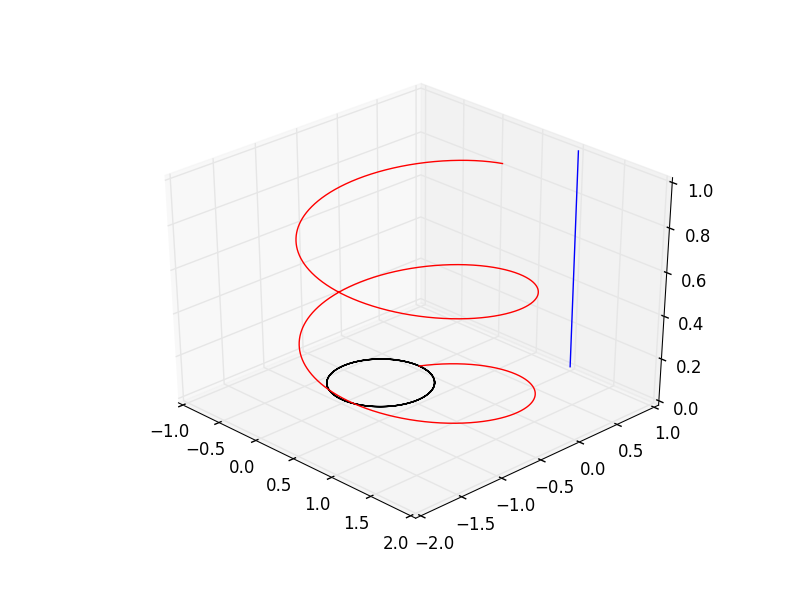
Here, we have three particle trajectories in a constant magnetic field. The black trajectory is a particle traveling wholly perpendicular to the magnetic field—its path is a circle, as expected. The red path is a particle with velocity components both parallel to and perpendicular to the field, resulting in a helix—it also has a greater mass, which results in a wider curvature of path. The blue line is a particle traveling completely parallel to the force—its motion is not affected at all.
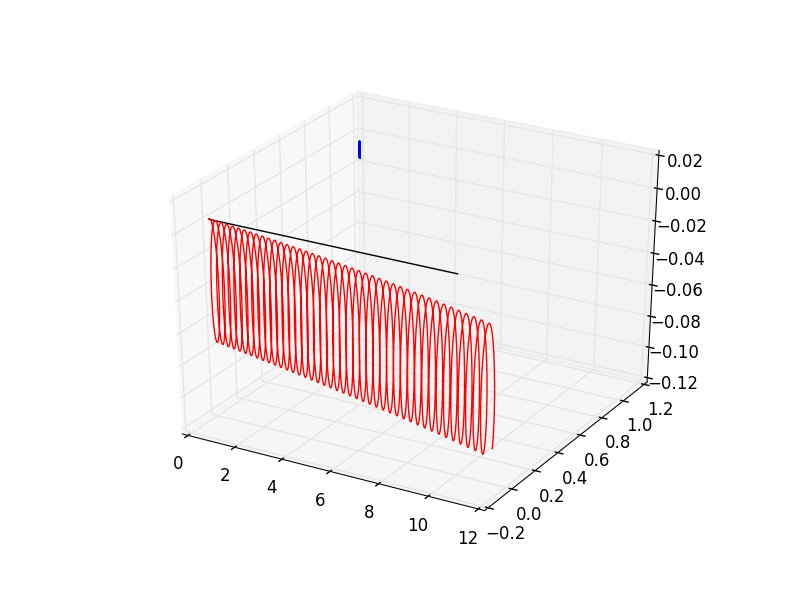
With a wackier, arbitrary B field (b = np.array([2, 0, .1*z]), we get something sillier:
E Fields
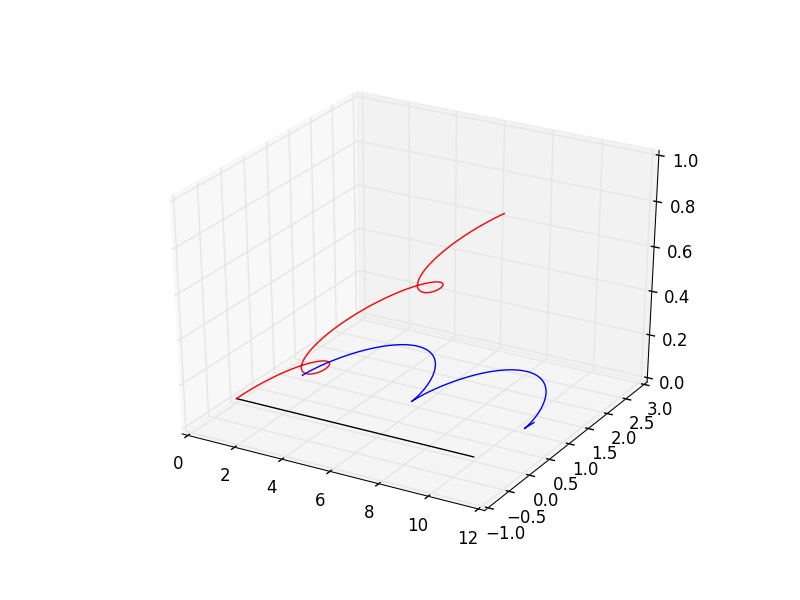
The fun doesn't stop there...we can handle E fields too! Take a look at the next example, with a constant E field. Note the blue path, a particle that starts at rest, approximates cycloid motion! Cycloids are really, really cool for a lot of reasons (they're solutions to both the tautochrone and brachistochrone problems! I'm so excited!).
LET'S GET CRAZY
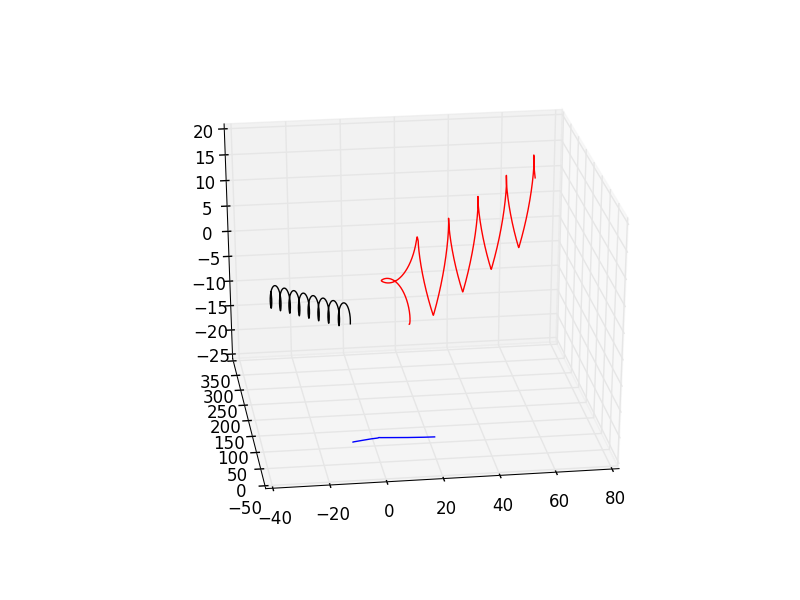
We added a point charge here, which doesn't actually exert enough force to do anything too funky, except for the weird loop that the start of the red trajectory.
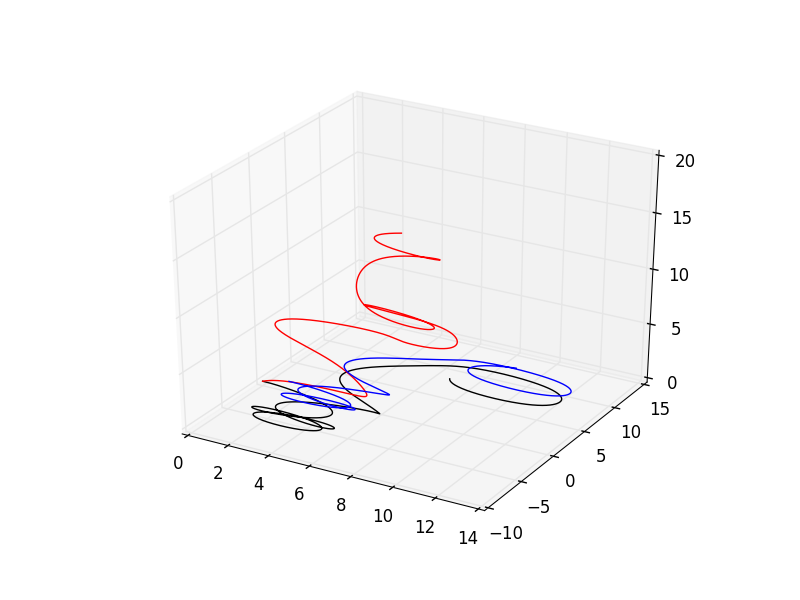
What happens if you use an E field of the form of a sin function? This. This happens.
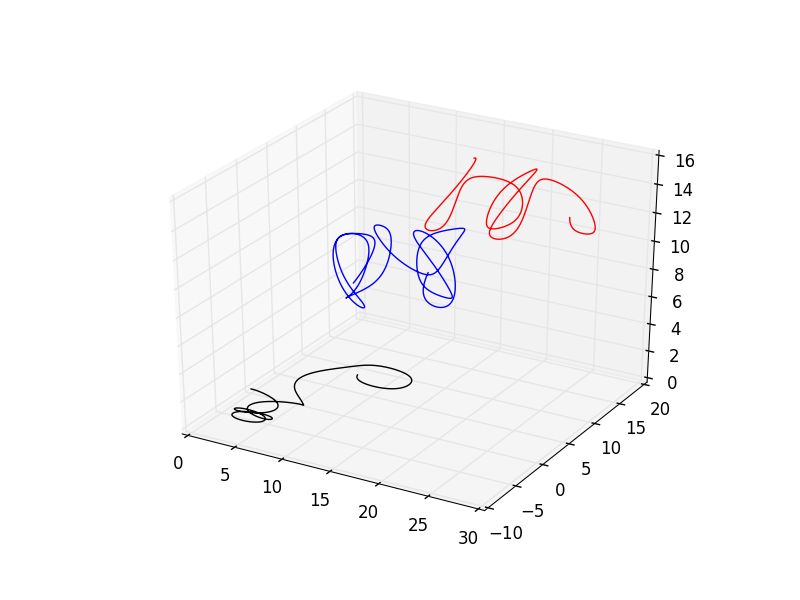
Now I'm just honestly messing around. But I'm having a good time.
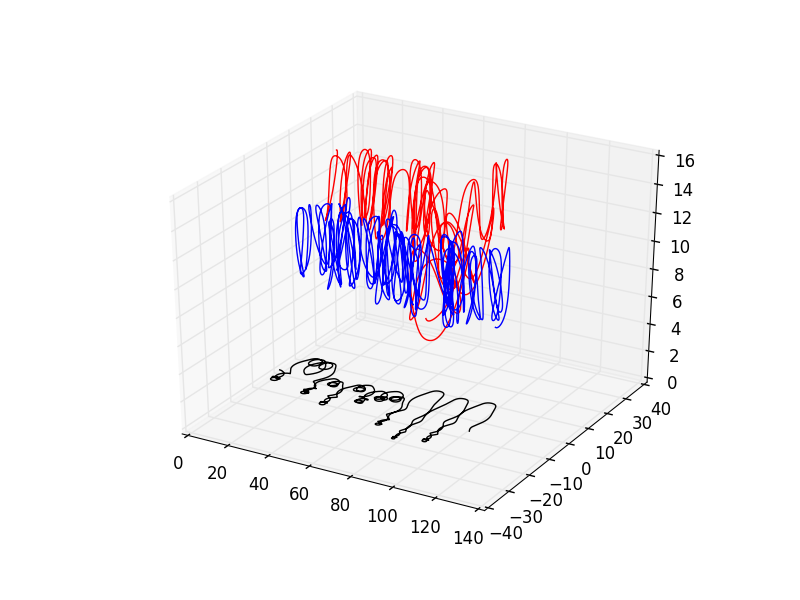
This is the same thing as last time, but I let it run for ten times as long. Woooooooah.